A Functional Which is Continuous is Lower Semicontinous
3.7: Lower Semicontinuity and Upper Semicontinuity
- Page ID
- 50130
The concept of semicontinuity is convenient for the study of maxima and minima of some discontinuous functions.
Let \(f: D \rightarrow \mathbb{R}\) and let \(\bar{x} \in D\). We say that \(f\) is lower semicontinuous (l.s.c.) at \(\bar{x}\) if for every \(\varepsilon > 0\), there exists \(\delta > 0\) such that
\[f(\bar{x})-\varepsilon<f(x) \text { for all } x \in B(\bar{x} ; \delta) \cap D .\]
Similarly, we say that \(f\) is upper semicontinuous (e.s.c.) at \(\bar{x}\) if for every \(\varepsilon > 0\), there exists \(\delta > 0\) such that
\[f(x)<f(\bar{x})+\varepsilon \text { for all } x \in B(\bar{x} ; \delta) \cap D .\]
It is clear that \(f\) is continuous at \(\bar{x}\) if and only if \(f\) is lower semicontinuous and upper semicontinuous at this point.
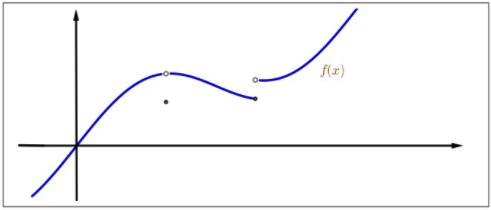
Figure \(3.6\): Lower semicontinuity.
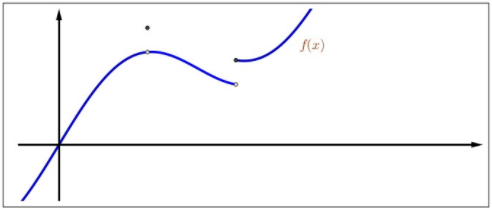
Figure \(3.7\): Upper semicontinuity.
Let \(f: D \rightarrow \mathbb{R}\) and let \(\bar{x} \in D\) be a limit point of \(D\). Then \(f\) is lower semicontinuous at \(\bar{x}\) if and only if
\[\liminf _{x \rightarrow \bar{x}} f(x) \geq f(\bar{x}) .\]
Similarly, \(f\) is upper semicontinuous at \(\bar{x}\) if and only if
\[\limsup _{x \rightarrow \bar{x}} f(x) \leq f(\bar{x}) .\]
- Proof
-
Suppose \(f\) is lower semiconitnuous at \(\bar{x}\). Let \(\varepsilon > 0\). Then there exists \(\delta_{0}>0\) such that
\[f(\bar{x})-\varepsilon<f(x) \text { for all } x \in B\left(\bar{x} ; \delta_{0}\right) \cap D .\]
This implies
\[f(\bar{x})-\varepsilon \leq h\left(\delta_{0}\right),\]
where
\[h(\delta)=\inf _{x \in B_{0}(\bar{x} ; \delta) \cap D} f(x) .\]
Thus,
\[\liminf _{x \rightarrow \bar{x}} f(x)=\sup _{\delta>0} h(\delta) \geq h\left(\delta_{0}\right) \geq f(\bar{x})-\varepsilon .\]
Since \(\varepsilon\) is arbitrary, we obtain \(\liminf _{x \rightarrow \bar{x}} f(x) \geq f(\bar{x})\).
We now prove the converse. Suppose
\[\liminf _{x \rightarrow \bar{x}} f(x)=\sup _{\delta>0} h(\delta) \geq f(\bar{x})\]
and let \(\varepsilon > 0\). Since
\[\sup _{\delta>0} h(\delta)>f(\bar{x})-\varepsilon ,\]
there exists \(\delta > 0\) such that \(h(\delta)>f(\bar{x})-\varepsilon\). This implies
\[f(x)>f(\bar{x})-\varepsilon \text { for all } x \in B_{0}(\bar{x} ; \delta) \cap D .\]
Since this is also true for \(x = \bar{x}\), the function \(f\) is lower semicontinuous at \(\bar{x}\).
The proof for the upper semicontinuous case is similar. \(\square\)
Let \(f: D \rightarrow \mathbb{R}\) and let \(\bar{x} \in D\). Then \(f\) is l.s.c. at \(\bar{x}\) if and only if for every sequence \(\left\{x_{k}\right\}\) in \(D\) that converges to \(\bar{x}\),
\[\liminf _{k \rightarrow \infty} f\left(x_{k}\right) \geq f(\bar{x}) .\]
Similarly, \(f\) is u.s.c. at \(\bar{x}\) if and only if for every sequence \(\left\{x_{k}\right\}\) in \(D\) that converges to \(\bar{x}\),
\[\limsup _{k \rightarrow \infty} f\left(x_{k}\right) \leq f(\bar{x}) .\]
- Proof
-
Suppose \(f\) is l.s.c. at \(\bar{x}\). Then for any \(\varepsilon > 0\), there exists \(\delta > 0\) such that (3.12) holds. Since \(\left\{x_{k}\right\}\) converges to \(\bar{x}\), we have \(x_{k} \in B(\bar{x} ; \delta)\) when \(k\) is sufficiently large. Thus,
\[f(\bar{x})-\varepsilon<f\left(x_{k}\right)\]
for such \(k\). It follows that \(f(\bar{x})-\varepsilon \leq \liminf _{k \rightarrow \infty} f\left(x_{k}\right)\). Since \(\varepsilon\) is arbitrary, it follows that \(f(\bar{x}) \leq \liminf _{k \rightarrow \infty} f\left(x_{k}\right)\).
We now prove the converse. Suppose \(\liminf _{k \rightarrow \infty} f\left(x_{k}\right) \geq f(\bar{x})\) and assume, by way of contradiction, that \(f\) is not l.s.c. at \(\bar{x}\). Then there exists \(\bar{\varepsilon}>0\) such that for every \(\delta > 0\), there exists \(x_{\delta} \in B(\bar{x} ; \delta) \cap D\) with
\[f(\bar{x})-\bar{\varepsilon} \geq f\left(x_{\delta}\right) .\]
Applying this for \(\delta_{k}=\frac{1}{k}\), we obtain a sequence \(\left\{x_{k}\right\}\) in \(D\) that converges to \(\bar{x}\) with
\[f(\bar{x})-\bar{\varepsilon} \geq f\left(x_{k}\right) \text { for every } \mathrm{k} .\]
This implies
\[f(\bar{x})-\bar{\varepsilon} \geq \liminf _{k \rightarrow \infty} f\left(x_{k}\right) .\]
This is a contradiction. \(\square\)
Let \(f: D \rightarrow \mathbb{R}\). We say that \(f\) is lower semicontinuous on \(D\) (or lower semicontinuous if no confusion occurs) if it is lower semicontinuous at every point of \(D\).
Suppose \(D\) is a compact set of \(\mathbb{R}\) and \(f: D \rightarrow \mathbb{R}\) is lower semicontinuous. Then \(f\) has an absolute minimum on \(D\). That means there exists \(\bar{x} \in D\) such that
\[f(x) \geq f(\bar{x}) \text { for all } x \in D .\]
- Proof
-
We first prove that \(f\) is bounded below. Suppose by contradiction that for every \(k \in \mathbb{N}\), there exists \(x_{k} \in D\) such that
\[f\left(x_{k}\right)<-k .\]
Since \(D\) is compact, there exists a subsequence \(\left\{x_{k_{\ell}}\right\}\) of \(\left\{x_{k}\right\}\) that converges to \(x_{0} \in D\). Since \(f\) is l.s.c., by Theorem 3.7.2
\[\liminf _{\ell \rightarrow \infty} f\left(x_{k_{\ell}}\right) \geq f\left(x_{0}\right) .\]
This is a contraction because \(\liminf _{\ell \rightarrow \infty} f\left(x_{k_{\ell}}\right)=-\infty\). This shows \(f\) is bounded below. Define
\[\gamma=\inf \{f(x): x \in D\} .\]
Since the set \(\{f(x): x \in D\}\) is nonempty and bounded below, \(\gamma \in \mathbb{R}\).
Let \(\left\{u_{k}\right\}\) be a sequence in \(D\) such that \(\left\{f\left(u_{k}\right)\right\}\) converges to \(\gamma\). By the compactness of \(D\), the sequence \(\left\{u_{k}\right\}\) has a convergent subsequence \(\left\{u_{k_{\ell}}\right\}\) that converges to some \(\bar{x} \in D\). Then
\[\gamma=\lim _{\ell \rightarrow \infty} f\left(u_{k_{\ell}}\right)=\liminf _{\ell \rightarrow \infty} f\left(u_{k_{\ell}}\right) \geq f(\bar{x}) \geq \gamma .\]
This implies \(\gamma=f(\bar{x})\) and, hence,
\[f(x) \geq f(\bar{x}) \text { for all } x \in D .\]
The proof is now complete. \(\square\)
The following theorem is proved similarly.
Suppose \(D\) is a compact subset of \(\mathbb{R}\) and \(f: D \rightarrow \mathbb{R}\) is upper semicontinuous. Then \(f\) has an absolute maximum on \(D\). That is, there exists \(\bar{x} \in D\) such that
\[f(x) \leq f(\bar{x}) \text { for all } x \in D .\]
For every \(a \in \mathbb{R}\), define
\[\mathscr{L}_{a}(f)=\{x \in D: f(x) \leq a\}\]
and
\[\mathscr{L}_{a}(f)=\{x \in D: f(x) \leq a\} .\]
- Proof
-
Add proof here and it will automatically be hidden
Let \(f: D \rightarrow \mathbb{R}\). Then \(f\) is lower semicontinuous if and only if \(\mathscr{L}_{a}(f)\) is closed in \(D\) for every \(a \in \mathbb{R}\). Similarly, \(f\) is upper semicontinuous if and only if \(\mathscr{U}_{a}(f)\) is closed in \(D\) for every \(a \in \mathbb{R}\).
- Proof
-
Suppose \(f\) is lower semicontinuous. Using Corollary 2.6.10, we will prove that for every sequence \(\left\{x_{k}\right\}\) in \(\mathscr{L}_{a}(f)\) that converges to a point \(\bar{x} \in D\), we get \(\bar{x} \in \mathscr{L}_{a}(f)\). For every \(k\), since \(x_{k} \in \mathscr{L}_{a}(f)\), \(f\left(x_{k}\right) \leq a\).
Since \(f\) is lower semicontinuous at \(\bar{x}\),
\[f(\bar{x}) \leq \liminf _{k \rightarrow \infty} f\left(x_{k}\right) \leq a .\]
Thus, \(\bar{x} \in \mathscr{L}_{a}(f)\). It follows that \(\mathscr{L}_{a}(f)\) is closed.
We now prove the converse. Fix any \(\bar{x} \in D\) and \(\varepsilon > 0\). Then the set
\[G=\{x \in D: f(x)>f(\bar{x})-\varepsilon\}=D \backslash \mathscr{L}_{f(x)-\varepsilon(f)}\]
is open in \(D\) and \(\bar{x} \in G\). Thus, there exists \(\delta > 0\) such that
\[B(\bar{x} ; \delta) \cap D \subset G .\]
It follows that
\[f(\bar{x})-\varepsilon<f(x) \text { for all } x \in B(\bar{x} ; \delta) \cap D .\]
Therefore, \(f\) is lower semicontinuous. The proof for the upper semicontinuous case is similar. \(\square\)
For every \(a \in \mathbb{R}\), we also define
\[L_{a}(f)=\{x \in D: f(x)<a\}\]
and
\[U_{a}(f)=\{x \in D: f(x)>a\} .\]
Let \(f: D \rightarrow \mathbb{R}\). Then \(f\) is lower semicontinuous if and only if \(U_{a}(f)\) is open in \(D\) for every \(a \in \mathbb{R}\). Similarly, \(f\) is upper semicontinuous if and only if \(L_{a}(f)\) is open in \(D\) for every \(a \in \mathbb{R}\).
- Proof
-
Add proof here and it will automatically be hidden
Let \(f: D \rightarrow \mathbb{R}\). Then \(f\) is continuous if and only if for every \(a,b \in \mathbb{R}\) with \(a < b\). the set
\[O_{a, b}=\{x \in D: a<f(x)<b\}=f^{-1}((a, b))\]
is an open in \(D\).
- Proof
-
Suppose \(f\) is continuous. Then \(f\) is lower semicontinuous and upper semicontinuous. Fix \(a,b \in \mathbb{R}\) with \(a < b\). Then
\[O_{a, b}=L_{b} \cap U_{a} .\]
By Theorem 3.7.6, the set \(O_{a, b}\) is open since it is the intersection of two opens sets \(L_{a}\) and \(U_{b}\).
Let us prove the converse. We will only show that \(f\) is lower semicontinuous since the proof of upper semicontinuity is simiilar. For every \(a \in \mathbb{R}\), we have
\[U_{a}(f)=\{x \in D: f(x)>a\}=\cup_{n \in \mathbb{N}} f^{-1}((a, a+n))\]
Thus, \(U_{a}(f)\) is open in \(D\) as it is a union of open sets in \(D\). Therefore, \(f\) is lower semicontinuous by Corollary 3.7.6. \(\square\)
Exercise \(\PageIndex{1}\)
Let \(f\) be the function given by
\[f(x)=\left\{\begin{array}{ll}
x^{2}, & \text { if } x \neq 0 \text {;} \\
-1, & \text { if } x=0 \text {.}
\end{array}\right .\]
Prove that \(f\) is lower semicontinuous.
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{2}\)
Let \(f\) be the function given by
\[f(x)=\left\{\begin{array}{ll}
x^{2}, & \text { if } x \neq 0 \text {;} \\
1, & \text { if } x=0 \text {.}
\end{array}\right .\]
Prove that \(f\) is upper semicontinuous.
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{3}\)
Let \(f, g: D \rightarrow \mathbb{R}\) be lower semicontinuous functions and let \(k > 0\) be a constant. Prove that \(f + g\) and \(kf\) are lower semicontinuous functions on \(D\).
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{4}\)
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a lower semicontinuous function such that
\[\lim _{x \rightarrow \infty} f(x)=\lim _{x \rightarrow-\infty} f(x)=\infty .\]
Prove that \(f\) has an absolute minimum at some \(x_{0} \in \mathbb{R}\).
- Answer
-
Add texts here. Do not delete this text first.
dibenedettopecied.blogspot.com
Source: https://math.libretexts.org/Bookshelves/Analysis/Introduction_to_Mathematical_Analysis_I_%28Lafferriere_Lafferriere_and_Nguyen%29/03:_Limits_and_Continuity/3.07:_Lower_Semicontinuity_and_Upper_Semicontinuity

0 Response to "A Functional Which is Continuous is Lower Semicontinous"
Post a Comment